朝闻道

idea extraction

首页 归档 标签 关于

关于Vanilla Transformer的种种细节

2021-06-30 14 min read # transformer # DL


这部分内容不涉及BERT等后续网络和发展演进，仅涉及原教旨transformer。

网络结构简述

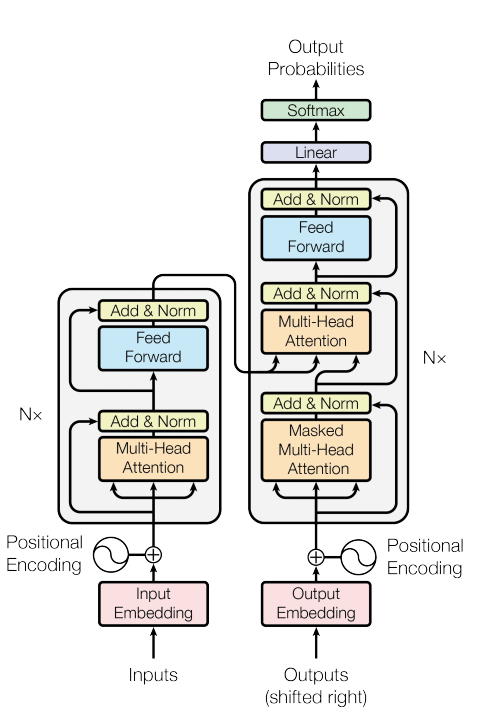
Transformer网络结构包含encoder与decoder两部分：

  • encoder由6个encoder layer构成，每个layer包含self-attention，FFN两大部分
  • decoder由6个decoder layer构成，每个layer包含self-attention，encoder-decoder attention，FFN三部分

embedding层、encoder layer、decoder layer以及子层 self-attention、encoder-decoder attention, FFN的输入输出维度相同。

Transformer最早用于翻译模型，所以在decoder段加入了linear layer+softmax进行token预测。

encoder 与 decoder embedding

encoder与decoder的embedding由 token embedding 和位置编码相加获得。

encoder/decoder embedding=token embedding+positional encoding\text{encoder/decoder embedding} = \text{token embedding} + \text{positional encoding}

decoder与encoder的 token embedding 层也可以构建在同一个词表中，来共享两种语言体系的中数字、字母和特殊符号这些共同表达。相应地，softmax层的计算量随之变大。

decoder的token embedding与decoder的输出层linear层可以认为是共享权重。这个参数共享可以降低参数量，两者可以认为是互逆的关系。

positional encoding

transformer的网络结构中缺乏序列信息，所以需要额外在embedding基础上增加序列编码

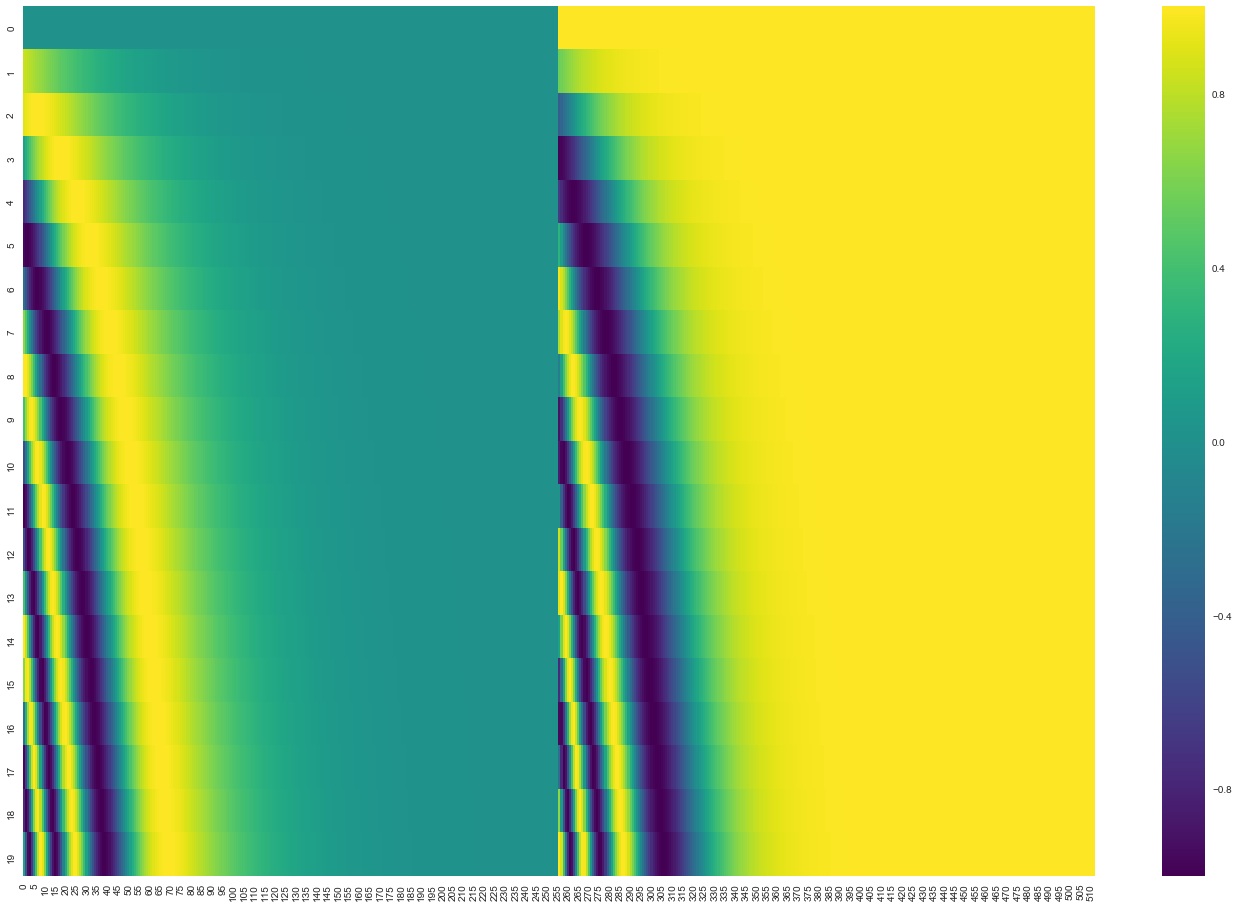
PE(pos,d)=sin⁡(pos100002×floor(d/2)dmodel+π2×(d mod 2))\text{PE}(\text{pos}, \text{d}) = \sin (\frac{\text{pos}}{10000^{\frac{2 \times \text{floor}(\text{d}/2)}{d_{\text{model}}}}} + \frac{\pi}{2}\times (d \bmod 2))

引用Jay Alammar大佬画的图，下图表示的是一个seqlen为20（纵轴），dimension为512（横轴）的positional encoding的可视化效果。

Attention

Attention本质上是一种特征加权融合的方式，在神经网络中使用这种非线性融合结构可以将独立的局部特征转为更细腻有效的全局性特征。
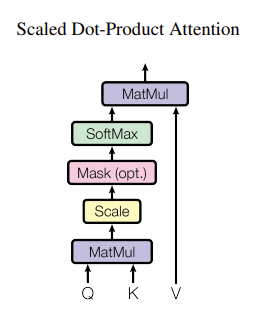
在Transformer中，Attention的基本结构是 Scaled Dot-Product Attention，在每个Attention子层，原作者并行使用了多个相同的这种基本结构，称之为Multi-Head Attention，每个Head对应一个基本结构。
这样在训练过程，每个并行基本结构中的参数矩阵相互独立得更新，学习全局特征的构建方式。

MultiHead(X)=Linear(Concat(H1(X),H2(X),H3(X)...Hh(X)))\text{MultiHead}(X) = \text{Linear}(\text{Concat}(H_1(X), H_2(X), H_3(X)... H_h(X)))

这里面需要学习的参数包括各个Head中Scaled Dot-Product Attention使用的参数，以及Linear层中的矩阵。

Scaled Dot-Product Attention

Attention(Q,K,V)=softmax(QKTdk)V\text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V

Q=WqX,K=WkX,V=WvXQ= W_qX, K=W_kX, V=W_vX

masking

在训练翻译模型时，通过把QKTQK^T矩阵中未知位置设定为−∞-\infin，避免信息泄露。

encoder-decoder attention

在decoder中的encoder-decoder attention中，Query Q的输入来自于decoder部分的self attention的输出，而Key K和Value V的输入来自于encoder部分最后一层的输出。

FFN (Position-wise Feed-Forward)

其输入是encoder中self-attention输出与decoder中encoder-decoder attention的输出。对于每个位置的向量表达通过如下网络结构, (W1∈Rh×d,W2∈Rd×h,d=2048W_1 \in \reals^{h \times d}, W_2 \in \reals^{d \times h}, d=2048)

FFN(x)=Relu(xW1+b1)W2+b2\text{FFN}(x) = \text{Relu}(xW_1 + b_1) W_2 + b_2

Add & Norm

在每个Attention子层与FFN子层后，加入了残差网络和Norm操作：

H=LayerNorm(Attention(X)+X)H = \text{LayerNorm}(\text{Attention}(X) + X)

H=LayerNorm(FFN(X)+X)H = \text{LayerNorm}(\text{FFN}(X) + X)

Dropout

Vanilla Transformer的dropout在网络中位于：

  • 子层(attention, FFN)计算之后，Add&Norm之前
  • encoder/decoder embedding之后

learning rate scheduler：Noam

这个优化策略融合了warmup和learning rate decay的机制，就命名看大概率是二作贡献的优化方案。

lr=min⁡(step_num−0.5,step_num×warmup_steps−1.5)dmodellr=\frac{\min(\text{step\_num}^{-0.5}, \text{step\_num} \times \text{warmup\_steps}^{-1.5})}{\sqrt{d_{model}}}

细节

Vanilla Transformer的网络结构中很多细节在受关注后学界进行了分析实验，还有一些细节来自于此前的一些研究工作，这里整理一下。

token词表构建：bpe & word-piece

vanilla Transformer在不同的翻译任务中使用了两种不同的subword算法: byte pair encoding 和 word-piece 算法。
bpe是一个串行算法，

  1. 首先把语料中的词切为字母粒度，
  2. 然后统计相邻子词一起出现的频率，
  3. 选择频率最高子词对的加入词表，
  4. 以此新词表更新语料分词结果
  5. 迭代执行2-4步更新词表，直到达到目标词汇表规模。

其论文中举例描述了算法，参考它的图例

在编码时，bpe首先把句子切分为字母粒度，然后从长到短遍历词表，将匹配到的相邻字母序列拼接为子词。
在huggingface的实现中，bpe会先把word切为character粒度子词，然后逐渐把在表格中的相邻子词两两拼接起来，直到相邻子词拼接后不在词表中。

word-piece算法与bpe类似，区别在于step3，word-piece没有选择频率最大的相邻子词，而选择能使训练语料似然值上升最大的。
word-piece没有放出源码，在具体如何实现见仁见智。原文是用的是NGram统计语言模型做打分，而huggingface发布的tonkenizer中word-piece直接使用了bpe的训练方法。在这篇知乎文章里，则基于独立假设将“求语料似然值提升最大相邻子词”转化为选择为相邻子词的互信息最大。

在huggingface的实现中，word-piece的编码过程是一个贪婪算法，首先优先匹配整个词。如果找不到，则回退end指针，尝试匹配跟短的token，如此逐步将word拆分为多个子词。

参数共享：Weight Tying

论文Using the Output Embedding to Improve Language Models验证了在翻译模型中，将embedding层和映射层进行参数共享，可以在降低模型参数量的同时，保持模型效果稳定。
在Transformer中，使用了weight typing的位置包括：

  • decoder embedding 与 decoder FC layer(before softmax)
  • encoder embedding 与 decoder embedding
    第二种是两种语言的词表混合，两种语言共用的token会得到更充分的训练，也可以覆盖到一些语言混合表达场景。

激活函数：Relu vs Gelu

Vanilla Transformer使用的激活函数是Relu，而后续的一些改进方案中使用了16年发表的Gelu。其设计受Dropout和Relu启发，认为两者操作本质上都是输入与0-1 mask相乘。由此作者设计了一种新的激活函数：

  • 将input与Bernoulli分布期望相乘
  • 而Bernoulli分布的参数也是一个受input影响的变量，这里设计为标准高斯分布的CDF（单调递增）
  • 作者认为神经元的输入受Batch/Layer Normalization修正，一般满足高斯分布假设。也就是随着输入越大，则CDF变大，Bernoulli分布输出1的概率越大。

Gelu(x)=x×E(Bernoulli(CDF(x)))=x×1×CDF(x)+x×0×(1−CDF(x))\text{Gelu}(x) = x \times E(\text{Bernoulli}(\text{CDF}(x))) = x \times 1 \times \text{CDF}(x) + x \times 0 \times (1 - \text{CDF}(x))

Gelu(x)=x×CDF(x)=x×1+erf(x/2)2\text{Gelu}(x) = x \times \text{CDF}(x) = x \times \frac{1 + \text{erf}(x/\sqrt{2})}{2}

FFN与Memory Network

论文Transformer Feed-Forward Layers Are Key-Value Memories中将Transformer中的FFN与Key-Value Memory Network做关联讨论。
此前学界提出的Memory Network是一种神经网络中的长效存储机制，相对于LSTM等神经网络通过网络结构设计进行记忆信息的传递，Memory Network将参考背景信息来进行非线性特征融合的一种结构，在一些类似多轮对话的场景中，背景信息编码会常常随着对话进行而更新。
Key-Value Memory Network就是其中一种MN网络设计，其计算方法如下：

MN(x)=softmax(xKT)V\text{MN}(x) = \text{softmax}(x K^T)V

而在Transformer中的FFN，可以写为：

FFN(x)=Relu(xKT)V\text{FFN}(x) = \text{Relu}(x K^T)V

其中K,V∈Rdm×dK,V \in \reals^{d_m \times d}
从表达形式上看，FFN与KV MN仅在激活函数上有所区别。基于FFN≃KV-MN\text{FFN} \simeq \text{KV-MN}这个假设，论文做了一系列KV MN性质的数据分析，这里整理下实验分析结论：

  • 观察Relu(xKT)\text{Relu}(x K^T)的激活程度：
    • Key Matrix中每个dd维子向量表示，都与人类可识别的语言模式/规律相关
    • 浅层提取更明显的浅层语言模式，这里指N-Gram特征，而更深层提取更多的主题特征
  • 将Value Matrix中每个dd维向量与Output Embedding相乘对词表做Softmax，转化为分布：
    • 随着深度加深，Value Vector在词表上的分布与其对应维度的Key Vector激活词的next token相关度上升

FFN在BERT结构里面扮演着核心角色，个人看法，正是FFN的记忆能力使NLP从语言模式学习进入了大规模预训练的阶段。此前有一篇文章Language models are open knowledge graphs尝试过使用匹配打分的方法，用预训练模型从文本中无监督挖掘潜在的三元组。从文章给出的结果看，模型隐层维度H与抽取效果F1呈正相关关系。开个脑洞，如果将FFN视为KV MN，将中间层维度增大也许可以取得更好的提升效果。

增强 Multi-Head 多样性

https://arxiv.org/pdf/1810.10183.pdf

scale的作用

关于scale的作用，Tianyang Lin在知乎的答案目前是看到最清晰完整的解释。简单汇总下答案思路：

  • 首先，对于softmax来说，输入的数值数量级越大，通过exp放大其最大值对应输出越趋近于1。而softmax在输出趋近one hot时，梯度计算接近0，呈现梯度消失现象
  • 其次，在使用softmax计算attention权重时，需要避免梯度消失、爆炸阻断反向传播。
  • 假设k，q的mean和variance分别为0和1，而其内积mean=0，variance=dk\text{mean}=0， \text{variance}=d_k
  • 最终通过scale=dk\text{scale}=\sqrt{d_k}放缩，内积产生的variance放大作用被消除，“内积 + 放缩”单元的输入输出分布特征相同，因内积产生的梯度消失问题得以解决。

position encoding的性质

https://arxiv.org/pdf/1911.04474.pdf

参数初始化：xavier

良好的初始化可以保证在训练早期不会出现梯度爆炸和消失。在这篇blog文章Weight Initialization in Neural Networks: A Journey From the Basics to Kaiming中作者做了相关实验，证明在使用Tanh函数时配合Xavier Initialization可以保证深度神经网络的输入和输出分布在前向和后向计算时方差稳定，使用Relu作为激活函数则宜配合使用Kaiming Initialization.
在vanilla transformer中使用了xavier初始化进行参数初始化即

W∈Rdi×do∼Uniform(−γ,γ),γ=6di+doW \in \reals^{d_i \times d_o} \sim \text{Uniform}(-\gamma, \gamma), \gamma = \sqrt{\frac{6}{d_i + d_o}}

bias一般在实现中初始化为0.

Initializing the biases. It is possible and common to initialize the biases to be zero, since the asymmetry breaking is provided by the small random numbers in the weights. For ReLU non-linearities, some people like to use small constant value such as 0.01 for all biases because this ensures that all ReLU units fire in the beginning and therefore obtain and propagate some gradient. However, it is not clear if this provides a consistent improvement (in fact some results seem to indicate that this performs worse) and it is more common to simply use 0 bias initialization.
-- cs231n

此后，陆续有一些针对transformer参数初始化的新方案被提出来，以降低优化难度、简化网络结构：

感兴趣的朋友可以去阅读下看看。

References

Photo by Samule Sun on Unsplash

Powered by Gridea RSS